1. Implementación de la actividad

1.1. Objetivo

• Determinar las dificultades presentadas en los estudiantes de séptimo grado en  la comprensión de los conceptos geométricos sobre transformaciones rígidas bidimensionales, con el fin  reducir  progresivamente dichas deficiencias conceptuales.

1.2. Competencia a desarrollar

• Predigo y comparo los resultados de aplicar transformaciones rígidas (traslaciones, rotaciones, reflexiones) y homotecias (ampliaciones y reducciones) sobre figuras bidimensionales en situaciones matemáticas y en el arte.

1.3.  Tiempo estimado para el desarrollo del curso/unidad

• Se tiene estipulado una duración de cuatro sesiones de clase, cada una con una duración de dos horas de trabajo presencial  (fecha inicio: 01/10/2018; fecha fiscalización: 26/10/2018).

1.4. Conceptos claves

• Transformaciones rígidas, rotación, traslación, rotación, GeoGebra. 

1.5. Conceptos teóricos

LAS TRANSFORMACIONES RÍGIDAS

Traslación 

Una traslación es una transformación que consiste en desplazar una figura a lo largo de una línea recta conservando la longitud de sus lados y la medida de sus ángulos. Para de terminar la traslación de una figura es necesario indicar la dirección, es decir como puede ser el movimiento horizontal o vertical. El sentido de una traslación indica la orientación del movimiento y puede ser arriba, abajo, derecha o izquierda. Y la magnitud nos indica la cantidad de unidades de medida que se debe mover la figura, puede ser cualquier número natural.

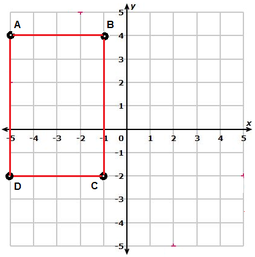
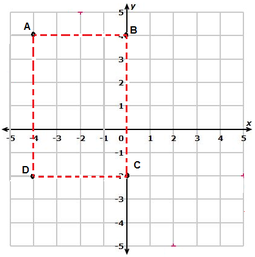
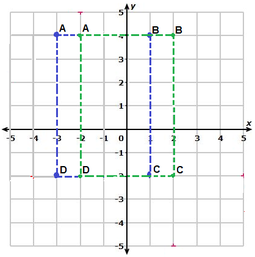
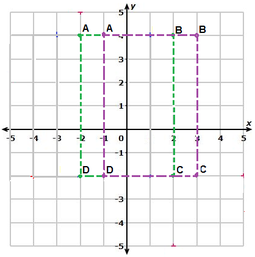
      EJEMPLO: Trasladar el rectángulo ABCD, cuatro unidades hacia la derecha.

• Lo primero es observar en que posición se encuentra el rectángulo inicialmente. Observemos que sus lados AD y BC, pasan inicialmente por los puntos -5 y -1 del eje de las abscisas o eje X.

• Luego vamos a desplazar cada uno de los vértices del rectángulo, es decir, los puntos ABCD, primero una posición hacia la derecha. Observemos que los lados AB y CD se han desplazado una posición hacia la derecha, ahora se encuentran sobre los puntos -4 y 0 del eje X.

• Continuamos con el desplazamiento de la figura hacia la derecha otra posición. primero se encuentran dichos lados en las posiciones -3 y 1 y luego tras mover el rectángulo otra vez se observa que la figura queda en las posiciones -2 y 2. Al final el movimiento de la figura de color verde se ha desplazado 3 unidades hacia la derecha.

• Por último movemos la figura una posición más y así se ubicaran los lados en las posiciones -1 y 3, esta es la posición final del rectángulo después de haberlo trasladado cuatro unidades hacia la derecha.

• Posición final.

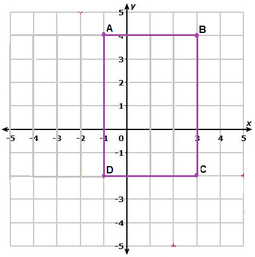
Rotación

La rotación es una transformación en el plano, que consiste en girar una figura al rededor de un punto, la rotación está determinada por una amplitud, una orientación y un centro de rotación. Para rotar una figura, es necesario indicar el ángulo de giro, el sentido (que puede ser en el sentido de las manecillas del reloj o en sentido contrario de las manecillas del reloj) y el punto sobre el cual se va a rotar. A este punto se le llama centro de rotación y puede estar en el interior de la figura, en uno de sus vértices o en el exterior de ella.

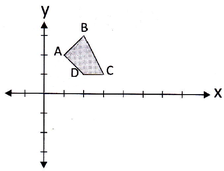
EJEMPLO: Rotar el cuadrilátero ABCD 90° en el sentido de las manecillas del reloj y al rededor del punto (0,0).

• El primer paso es unir cada uno de los vértices de la figura A, B, C, D, por medio de segmentos con el centro de rotación. 

• Luego con el transportador medimos la amplitud del ángulo dado, es decir 90°, a partir de cada segmento trazado, en el sentido de rotación indicado.

• Después trazamos con la ayuda de un compás medimos segmentos congruentes con cada segmento inicial, para luego ubicarlos en los vértices de la imagen.

• Por último se unen con segmentos, los vértices consecutivos. A´ B´ C´ D´ es la imagen de ABCD por la rotación dada.

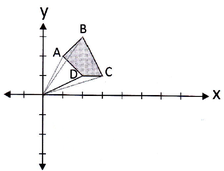
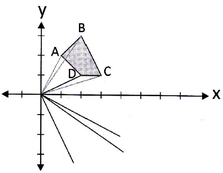
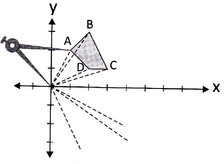
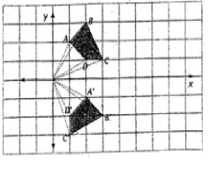
Reflexión 

La reflexión es una transformación rígida en el plano que consiste en dar media vuelta a una figura teniendo en cuenta una recta llamada eje de reflexión. 

La reflexión es el proceso de trasladar o copiar todos los puntos de una figura a otra posición equidistante (igual distancia) de una recta denominada eje de simetría (eje de reflexión). El resultado es una imagen especular (espejo) de la original. La reflexión de un figura se puede realizar de dos formas, la primera es realizar la reflexión sobre uno de sus vértices, y la segunda es realizar la sobre un punto diferente a sus vértices (fuera de la figura).

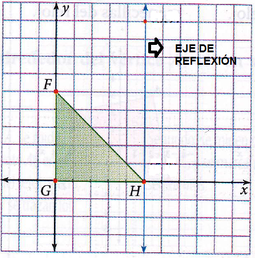
EJEMPLO: Reflejar el triángulo cuyos vértices  son FGH, sobre el vértice H.

Lo primero es identificar el vértice H y luego trazar por dicho punto una recta perpendicular al eje X, como se muestra en la figura, dicha recta es el eje de reflexión.

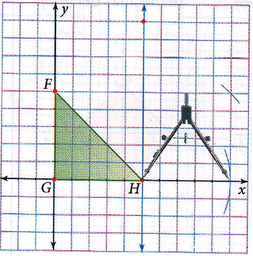
Después de haber trazado el eje de reflexión, con el compás se toma la medida desde el punto H que es por donde pasa el eje hasta cada uno de los vértices y sin mover el punto de apoyo del compás (punto H), se traslada cada medida al otro lado del eje para obtener la nueva figura.

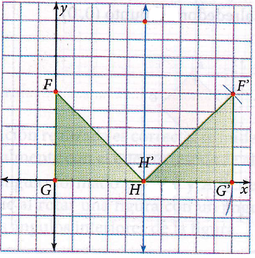
Después de haber marcado con el compás los vértices de la imagen, con una regla se unen para que quede la nueva figura.

Link descarga GeoGebra

1.6. Vídeo  manejo básico programa GeoGebra

1.7. Vídeo transformaciones rígidas

Simetría  

Traslación

Rotación 

1.7. Recursos 

Se trabaja con: diez portátiles, programa gratuito (GeoGebra), video tutorial y video Beam.

1.8.  Descripción 

No.	Descripción	Evaluación
1	Utilización  de GeoGebra: 1.      Descargar la aplicación gratuita a diez  portátiles institucionales. (Link de descarga: https://geogebra.softonic.com/descargar). 2.      Explicación básica a los estudiantes sobre los comandos del programa educativo. Así mismo, se puede presentar un vídeo tutorial (ver siguiente actividad opcional).  3.      Modelación amanuense  de situaciones problemas de la vida cotidiana (traslación, rotación, y reflexión de objetos tales como: cuadernos, mesas, pupitres, hojas de árboles, entre otros).  4.      Utilización guiada del software educativo para realizar la aplicación del punto tres. 5.      Resolución de interrogantes tanto del uso del software como de la temática trabajada en clase.  6.      Aplicación individual por parte de los estudiantes de los conceptos aprendidos, haciendo uso de GeoGebra, realizando cualquiera de las transformaciones rígidas bidimensionales. 7.      Retroalimentación colaborativa y obtención de      conclusiones de la actividad y conocimientos aprendidos o afianzados.	La evaluación se realiza de forma cuantitativa, donde los parámetros son estipulados en la rubrica de valoración propia para el desarrollo de la actividad.
2	Video  tutorial del uso de GeoGebra (opcional):        1.       Realizar la descarga o grabación del video tutorial de ser necesario del manejo general del software, donde se muestre el uso de los diferentes comandos y herramientas con que se cuenta (link video tutorial: https://www.youtube.com/watch?v=uAvGn6Toh6g). 2.      Presentación de la grabación para que los estudiantes realicen de forma práctica lo expuesto en el mismo.    3.      Dejar que exploren y aprendan otras funcionalidades de GeoGebra. 4.      Solicitar a cada estudiante realizar algo de lo aprendido, explicando a sus compañeros el procedimiento (se realiza la proyección del proceso con ayuda de video Beam). Obtener conclusiones y resolver inquietudes generales  del trabajo realizado.	Se utilizara como opción alternativa para fortalecer el uso básico de GeoGebra, siendo cualitativo, para su posterior cuantificación en la actividad relacionada con las trasformaciones rígidas bidimensionales.

 1.9. Rubrica de valoración

Rubrica de valoración de la actividad
Estándar: Predigo y comparo los resultados de aplicar transformaciones rígidas (traslaciones, rotaciones, reflexiones) y homotecias (ampliaciones y reducciones) sobre fi guras bidimensionales en situaciones matemáticas y en el arte.
Docente encargado: Licenciado Yesid Chivata.
Área: matemáticas – geometría.	Periodo: cuarto	Año:  2018
Desempeño	Valoración  cualitativa	Valoración cuantitativa
Bajo	Reconoce las transformaciones rígidas bidimensionales (traslación, rotación y reflexión).	De 1 a 2,9
Básico	Realiza uso de las características básicas de las transformaciones rígidas bidimensionales de forma correcta en situaciones específicas, aplicada en GeoGegra.	De 3,0 a 3,9
Alto	Relaciona las transformaciones rígidas bidimensional con situaciones de su diario vivir, haciendo uso adecuado de GeoGebra.	De 4,0 a 4,5
Superior	Plantea y resuelve en el programa GeoGebra nuevas situaciones problemas de la vida cotidiana, relacionado con las trasformaciones rígidas bidimensionales.	De 4,6 a 5,0
Nota: la valoración esta adecuada a los parámetros nacionales, estipulados por el Ministerio de Educación Nacional (MEN).